in this example, you will learn how to pan 16 audio tracks in a 5.1 surround environment using the lemur in conjunction with cubase sx. from basic x-y mapping to complex spatial pattern generation, this workshop provides an overview of lemur’s capabilities.

Controlling multi-channel panning us to be a nightmare. It makes no sense to use a knob for each panning direction. Even top of the range joystick-based controllers do not work that well when dealing with multiple audio tracks.

For sure, with any software-based audio sequencer, the best thing to do still seems to consist in drawing automation curves with a mouse.

The following tutorial highlights the various advantages of using the Lemur as an incredibly flexible and intuitive tool for sound spatialisation tasks. It describes a set of interfaces that illustrate different approaches of multi-channel panning.

In this example, the Lemur works in conjunction with Cubase SX(TM) . Any other professional sequencer would fit though.

When broadly considering the Lemur’s object library, you naturally tend to use the multiball object to control both left-right and rear-front panning.

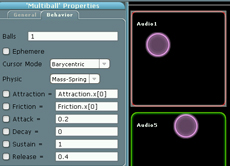
To start with, let’s create a multiball object called ‘Audio1’ and set its property as shown below.

Then, let’s map the X/Y coordinates of the ball to a pair of MIDI control change messages. For that purpose, hop to the MIDI panel. We’ll map the x coordinate of the ball to Control Change # 10and the y to Control change #11. Both messages are destinated to MIDI channel 1.

Now that the Lemur is sending the right messages, Cubase SX also needs setting up so as to assign CC10 and 11 to the LR and FR panning of the first audio track. Please refer to the Cubase User Manual to learn more about automation and control surface configuration.

Then, let’s duplicate the MultiBall seven times and reproduce the operation as shown above to control the 8 first audio tracks of Cubase Mixer. Note that for each track, you must change the MIDI channel.

Let’s add two MultiSliders so as to control the friction and attraction force of each MultiBall.

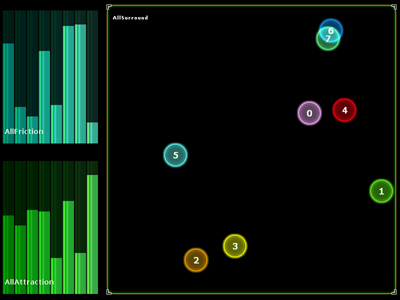
Another approche basically consists in using a single MultiBall, itself comprising 8 balls. Indeed, you might be more comfortable manipulating the 8 sound sources in a wider area.

Similarly, two multisliders are in charge of controlling the physical properties of each ball.

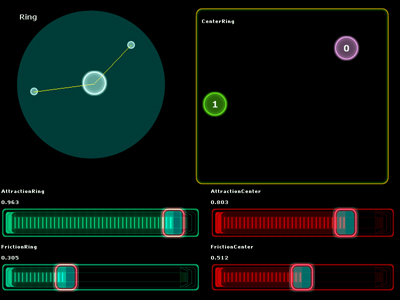
You might also find the RingArea to be very convenient.

In the example below, the Multiball controls the attractors of the RingArea. By playing with friction and attraction of both objects, you will achieve complex oscillations.

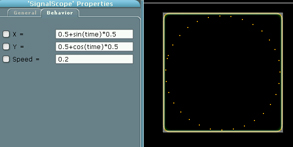
To end this overview let’s use the mathematical expression parser to generate automated trajectories.

The main object of this interface is the SignalScope, meant to display the resulting patterns. The X/Y parameters of the SignalScope are converted into a pair of MIDI control change messages.

Fisrt, let’s make the sound rotate in the diffusion space. We just need to type the following formula into the X and Y fields of the SignalScope:

X = 0.5+sin(time)*0.5
Y = 0.5+cos(time)*0.5

This way, the SignalScope will draw a circle as shown below.

Now, let’s control the following parameters of the elliptical trajectory: the center of the ellipse, its radius as well as it’s X/Y coefficient.

Let’s create a new Fader called Radius and change the SignalScope X/Y expressions:

X = 0.5+sin(time)*Radius.x/2
Y = 0.5+cos(time)* Radius.x/2

Then, let’s add a Multiball called Center and go back to the behavior window of the SignalScope:

X = Center.x+sin(time)*Radius.x/2
Y = Center.y+cos(time)* Radius.x/2

Thus, by moving the Center ball you will change the rotation center.

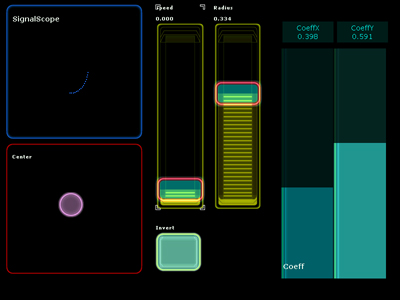
By creating a fader Freq, we can now control rotation speed:

X = Center.x+sin(2*pi*Freq.x*time)*Radius.x/2
Y = Center.y+cos(2*pi*Freq.x*time)* Radius.x/2

The MultiSlider – that will shall call ‘coeff’ – manages the X and Y coefficient to reshape the ellipse.

X=Coeff.x[0]*sin(2*pi*Freq.x*time)*Radius.x/2+Center.x
Y=Coeff.x[1]*cos(2*pi*Freq.x*time)*Radius.x/2+Center.y

Finally, a basic switch allows to invert the rotation direction. After creating the local variable Invert.out= range(x,-1,1), fill in the SignalScope X field with the following expression:

Invert.out*Coeff.x[0]*sin(2*pi*Freq.x*time)*Radius.x/2+Center.x